| Главная » Работы » Математика |
1. Найдем область определения
функции, для этого решим неравенство 2. Исследуем функцию на четность,
для этого найдем 3. Найдем нули функции, для этого 4. Найдем промежутки возрастания и
убывания функции. Для этого Значит
в точке  экстремум,
проверим максимум или минимум, для этого определим знак производной в
окрестности этой точки. экстремум,
проверим максимум или минимум, для этого определим знак производной в
окрестности этой точки.
Так как при
переходе через точку 5. Найдем точки перегиба и
промежутки выпуклости и вогнутости функции. Для этого Получаем точку
перегиба
Функция выпукла
на промежутках 6. Исследуем
график функции на поведение на бесконечности и в окрестности точек разрыва. При нахождении
области определения, мы установили, что функция имеет разрыв в точке Найдем
наклонные асимптоты. Наклонные асимптоты – это прямые и поэтому задаются
уравнением
7. Строим график функции
А(0;0)  | |||||||
| Просмотров: 2458 | Рейтинг: 0.0/0 | |||||||
| Всего комментариев: 0 | |
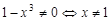 . Следовательно,
. Следовательно,  .
. . Следовательно, функция ни четная, ни нечетная.
Функция непериодичная.
. Следовательно, функция ни четная, ни нечетная.
Функция непериодичная.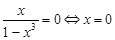 . Следовательно, график функции пересекает ось абсцисс
в точке
. Следовательно, график функции пересекает ось абсцисс
в точке  .
.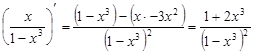 . Приравниваем производную к нулю
. Приравниваем производную к нулю 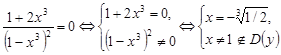 .
.
 и возрастает на
и возрастает на  , а точка будет минимумом. Найдем значении функции в
, а точка будет минимумом. Найдем значении функции в  . Итак
. Итак  .
. . Приравниваем вторую производную к нулю
. Приравниваем вторую производную к нулю 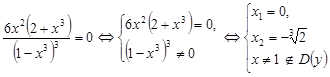 .
. . Определим промежутки выпуклости и вогнутости
функции, для этого определим знак второй производной в окрестности точки
перегиба.
. Определим промежутки выпуклости и вогнутости
функции, для этого определим знак второй производной в окрестности точки
перегиба.
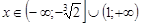
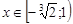

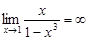



 и
и 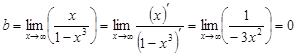 . Следовательно
. Следовательно 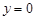 -
- 